Home
vinu.john.work.gmail.com https://github.com/vinujohn https://www.linkedin.com/in/vinu-john-9a95276/

Learning about neural networks with Go

by Vinu John,

In an effort to understand how neural networks work, I created one using the Go programming language without using any special frameworks or tools. The following is a digit recognizer application that sends a "drawn" image of a digit to a server, which classifies that image via a neural network.

Digit Recognizer

Recognizing Digits With A Neural Network

Recognizing handwritten digits using a neural network is considered by many to be the "Hello World" program of deep learning. One of the reasons why is that a dataset called the MNIST database is readily available to anyone who wants to try to build their own programs to recognize digits.

Wikipedia
By Suvanjanprasai - Own work, CC BY-SA 4.0, Wiki Commons

The MNIST database is a collection of 28-pixel wide by 28-pixel long grayscale images of handwritten digits curated by the National Institute of Standards and Technology for the purposes of training machines to recognize new handwritten digits it has not seen before. Around 60,000 images are provided for training, while another 10,000 images are provided for testing. Each grayscale image has pixel values of 0 to 255 to represent intensity. The MNIST images used for training and testing this particular neural network, can be found in the provided link, along with their associated labels.

The neural network code that I created can be found here. It allows you to create a fully connected network with an input layer of any size, a n number of hidden layers, and an output layer. This is commonly known as a multilayer perceptron neural network. Go is not as well known in the machine learning community as Python is, but I wanted to create something in my favorite programming language to understand the inner workings of neural networks without special machine learning frameworks or libraries. Also, neural network architectures like this one, are not really used anymore for image classification tasks since convolutional neural networks (CNNs) have much better performance. However, they are great to understand the fundamentals of deep learning.

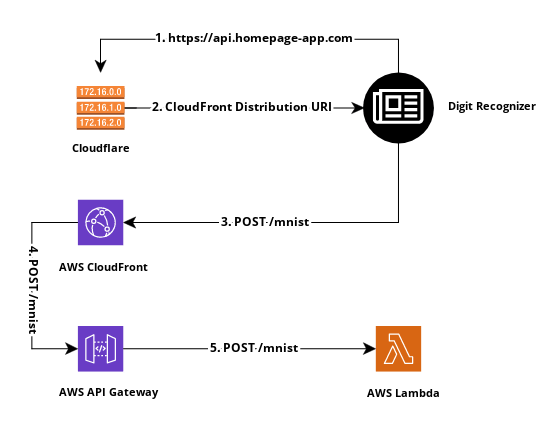
architecture
By Author

The model used in the digit recognizer has an accuracy of 96.72% with the MNIST testing set. It, along with the neural network code is used as a Go package in a GIN REST web service hosted with AWS Lambda behind AWS API Gateway and AWS CloudFront. Cloudflare is used to resolve the custom domain name and direct requests to the correct CloudFront distribution.

There are some key steps in building out a neural network. Since a neural network is composed of multiple layers of neurons (nodes), the network itself needs to accept a list of sizes for each layer, where a size represents the number of nodes in one layer. You need two layers at a minimum for input and output, and zero to many hidden layers. With this info, you should be able to construct the network so that each node in a successive layer has its own bias and a number of weights equal to the number of nodes in the previous layer. Either the same bias can be applied to every node in the same layer, or you can have individual biases for each node. The input layer is more of a logical construct than something modeled in code as individual nodes, since it is used to define the number of weights for each node in the first modeled layer.

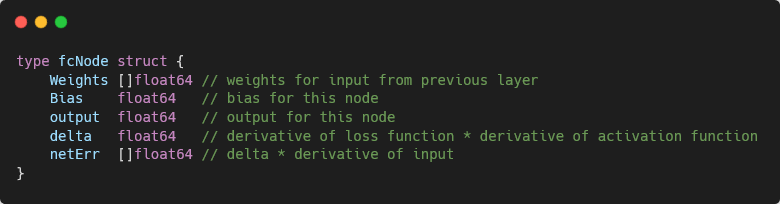
How you represent this information is up to you. I have seen implementations where multidimensional arrays are used to represent a weight by layer, then node, then weight. I found this confusing when performing different calculations, so I decided to create explicit node structures with their own weights and biases as members. After constructing the network, you will need to initialize the weights and biases with random values to help in the learning process.

By Author using carbon

You should also have two user operations in the API, which are train and predict. Predict is simple and uses a feed forward operation that applies the dot product to a previous layer's output and the current layer's node weights. A bias is also added for every node. The output of this calculation for each node is then fed into a non-linear activation function like Sigmoid and ReLU. The output of the activation function is in turn fed to the next layer of nodes, and the process happens all over again until all calculations for all nodes in each layer are complete. The output layer's final output is returned to the user as the prediction.

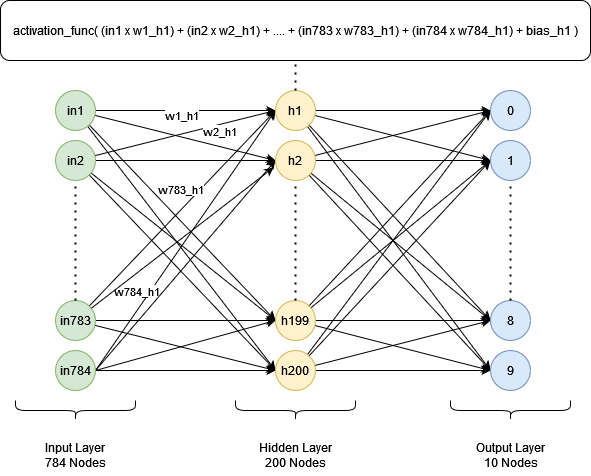
The network used for the digit recognizer is 784-200-10. 784 because the MNIST database uses 28-pixel by 28-pixel images, and 10 for the output because there are 10 digits in the decimal system. 200 was used for the hidden layer after some extensive testing, which I will go into later.

The following diagram shows how the feed forward operation would work with an example node (h1) in the hidden layer. Each input into h1 is multiplied by an individual weight and summed together along with a bias. This calculation is then used in an activation function whose output is used as input to the next layer.

By Author

The train operation is much more involved than predict. Training involves running a dataset of inputs through the feed forward operation of the network, and comparing outputs with corresponding target values. Once the outputs are compared with their respective target values, an error can be calculated for each node in the output layer so that the weights and biases of said node can be updated. For networks with more than 2 layers, the next layer before the output layer runs through the same process, using the errors calculated from the output layer to calculate its own error to update its own weights and biases. The process continues with each layer using the errors calculated from the next layer to update its weights and biases. This is known as backpropagation. The following is a rough outline of what training is actually doing for one row in the dataset:

  • Perform the feed forward operation to get outputs.
  • Calculate the error for each node in the output layer by comparing it with the target output for the row in question. In the case of MNIST, the target output will always be composed of 9 zeros and 1 one, which represents the digit that the network should recognize.
  • Take the error and decide how much each weight and bias in each node in the output layer needs to change, and then, in turn, figure out how the weights and biases of previous layer nodes need to change.
  • With all changes calculated, run through the network and apply updates to the weights and biases using the learning rate given to the train operation.

Each run through the dataset is called an epoch. Each epoch should keep track of the training loss so that you can see subsequent epochs minimizing that loss. If the loss gets larger or flatlines with subsequent epochs, you may decide to exit training early. The process of minimizing this loss is known as gradient descent.

Client Side

Digit Recognizer Image, By Author

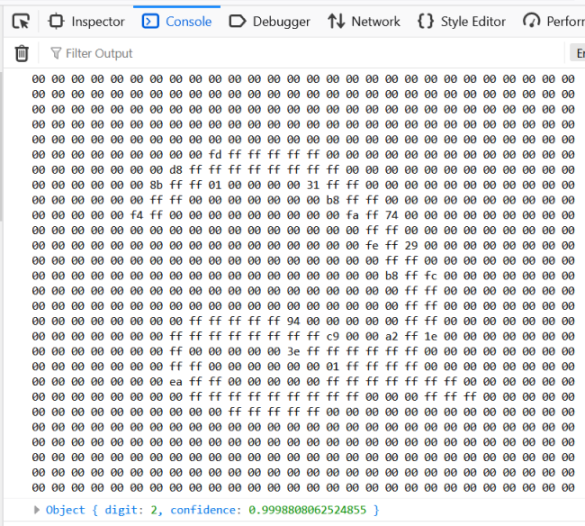
When viewing this page with your browser console open, any image sent to the server from the digit recognizer above will be logged along with the response from the server. This is helpful to visualize what exactly is being sent to the server and one can get a sense of what the neural network actually "sees," like the example shown. You can sort of make out the "2" in the log output if you stare at it long enough.

A big takeaway for me when learning about neural networks was that the correct input is key to successfully recognizing digits. In this case, a 280 x 280 PNG image from the drawing canvas in the digit recognizer, which is large enough for a human to draw on, is centered and then resized in the background when the user clicks 'Send', into a 28 x 28 PNG image, which is the correct input size for the neural network. The smaller PNG image is then converted to grayscale by taking only the alpha channel pixels from the image.

MNIST Image, By Author

When comparing the digit recognizer images to real handwritten MNIST images, they are not exactly the same. The pen "ink" in the digit recognizer is heavier, as if a person were pressing down heavily on the drawing surface causing image data values for those drawn pixels to be high. The stroke width of the pen itself does not match; the MNIST images seem to be more filled out on the 28 x 28 drawing space. This can all affect classification performance in a negative way, especially for digits that look similar. For example, recognizing the '7' and '9' digits seems to be hard since they look similar in the digit recognizer output. Even using the digit buttons is not always accurate. Clicking on different digit buttons with different browsers on different platforms, like desktop and mobile, can produce different results even though the same neural network and JavaScript client code are being used in both cases.

Training, Testing, and Refining on Repeat

One thing that you may notice when creating a neural network from scratch is that creating the neural network code is the easy part. Coming up with a trained network model with somewhat decent performance is the hard part. Your network needs to be continually trained with 60,000 MNIST images and tested with 10,000 MNIST test images until an acceptable performance profile is reached. This can be time consuming, so you want to make sure you have an automated training and testing plan. The training and testing code that I created can be found here.

During initial training, you want to make sure you are doing the following:

  • Start with smaller networks with one hidden layer that has a few nodes. This will reduce training time and allow you to adjust different parameters quickly, like the learning rate, so that you can get a better feel for what works and what doesn't. A learning rate of 0.01 is a good start. Research other people's network architecture in terms of layers and number of nodes plus the learning rate. You can then see if you are able to get similar performance.
  • Exit early from training when it makes sense to do so. You should definitely exit if the epoch that just finished has poorer performance with the testing set than the previous epoch. You may also want to exit early if the training loss increases from epoch to epoch.
  • Create a way that the network model can be saved after the completion of each epoch. This way, if training needs to exit early, you can use the latest model saved from training as your production model if it has decent performance. I used the Golang gob package to save and load models.

Training and testing are great ways to find problems with your network. During initial testing with the MNIST testing set, I could not achieve over 50% performance, much to my surprise. However, eventually, with the right changes to my neural network implementation, I was able to achieve much better performance. Some of these changes included:

  • Fixing issues with the input to the neural network by performing normalization. Normalizing the input by taking the [0, 255] pixel values and bringing them into the range of [0, 1] so that learning becomes faster.
  • Using a random uniform distribution for initializing the weights and biases of the network instead of a normal distribution since each digit outcome is equally likely.
  • Using Softmax vs. Sigmoid for the activation function in the output layer of the network which works better in multi-class problems like digit classification.

Resources

I could not do this project without help and I wanted to call out a couple of sites that I think are really worthwhile in learning neural networks: